
Řešení pravoúhlého trojúhelníku
Pravoúhlý trojúhelník počítaný goniometrickými funkcemi …
200 Kč
Popis
V online kurzu se naučíte počítat pravoúhlý trojúhelník pomocí goniometrických funkcí, rozlišovat hloubkový, výškový a zorný úhel.
Najdete zde 20 různých slovních úloh. Z toho dva příklady jsou písemnou formou komentované a 18 příkladů vypočtených krok za krokem. Všechny příklady obsahují přehledné náčrty.
Na závěr vás čeká 18 příkladů k procvičení.
Online kurz máte k dispozici po dobu jednoho měsíce.
Najdete zde např.:
1) Je dán rovnoramenný trojúhelník ABC. Známe stranu a = 50,3 cm a stranu c = 48,2 cm. Jak je daný trojúhelník vysoký? Jaké jsou jeho úhly?
2) Vrchol Eiffelovy věže je vidět pod výškovým úhlem 32°57′ ze vzdálenosti 500 metrů. Jaká je výška věže?
3) Zahrada tvaru obdélníku má délku kratší strany 15 metrů. Zahradu přepůlíme úhlopříčkou. Úhlopříčka svírá s delší stranou úhel 42°. Jaký je obsah zahrady?
Ukázka z kurzu
Nejdříve si zopakujeme, co už bychom měli z předchozího studia o pravoúhlém trojúhelníku znát.
Na obrázku vidíme pravoúhlý trojúhelník s vrcholy A, B, C. Vrcholy se popisují velkými tiskacími písmeny a popisujeme je v proti směru hodinových ručiček. Naproti vrcholu jsou strany trojúhelníku, které se označují malými psacími písmeny, shodnými s protilehlým vrcholem. Pravý úhel se vyskytuje tam, kde je jedna strana kolmá na stranu druhou.
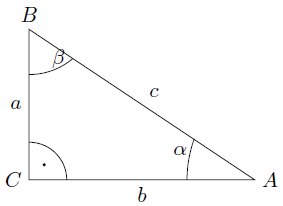
Nejdelší strana se nazývá přepona (v našem případě strana c). Zbývající strany jsou odvěsny.
Součet všech tří úhlů v trojúhelníku je vždy roven 180° (° čteme stupeň). Můžeme se také setkat se zadáním úhlů ve tvaru např. 45° 10′ 20“ (10′ 20“ čteme deset minut dvacet vteřin). Velikost pravého úhlu máme pevně stanovenou, tj. 90°. Úhly značíme písmeny řecké abecedy, nejčastěji alfa (\(\alpha\)), beta (\(\beta\)) a gama (\(\gamma\)).
Mezi goniometrické funkce patří:
a) funkce sinus (\(sin\)),
b) funkce kosinus (\(cos\)),
c) funkce tangens (\( tan \:nebo \:tg\)),
d) funkce kotangens (\( cotg\)),
