Přijímačky - test 1
Přijímačky - test 1
Závěrečný přehled
Zodpovězeno 0 z 14 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
Vyzkoušíte si své znalosti a časové dovednosti.
V našem zkušebním testu chybí rýsování – nezapomeňte si jej zopakovat.
Test obsahuje 14 otázek a můžete celkem získat 40 bodů.
Na test si udělejte čas 50 minut.
Nesmíte používat kalkulačku a tabulky. K dispozici můžete mít pouze papír, psací potřeby, své vědomosti a dobrou náladu.
Tak běžte do toho. Přejeme mnoho úspěchů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 14 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
-
Pokud Vám není nějaká odpověď jasná nebo si nevíte s některým příkladem rady, určitě nás kontaktujte.
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 14
1. Otázka
Bodové ohodnocení: 1Vypočtěte, o kolik větší je pětina čísla 13 než čtvrtina čísla 10.
(Výsledek uveďte v desetinném čísle)Správně
Špatně
pětina ze 13 – \(\dfrac{1}{5}\cdot 13\)
čtvrtina z 10 – \(\dfrac{1}{4}\cdot 10\)
o kolik = rozdíl
\(\dfrac{1}{5}\cdot 13-\dfrac{1}{4}\cdot 10=\dfrac{13}{5}-\dfrac{10}{4}\) -
Otázka 2 / 14
2. Otázka
Bodové ohodnocení: 3Vypočtěte:
2.1. \(100:\sqrt{4}+\sqrt{25}\cdot 3^2-3\cdot\sqrt{100-36}\)
2.2. \(\dfrac{\left(-\dfrac{2}{3}\right)^2\cdot\left(\dfrac{1}{7}\right)}{\left(\dfrac{3}{7}-1\dfrac{1}{2}\right):\dfrac{3}{8}}\)
Správně 3 / 3BodyŠpatně / 3 BodyMusíme dát pozor na to, jaké úpravy mají přednost – závorky, umocnění, odmocnění, násobení, dělení, sčítání, odčítání
2.1. \(100:2+5\cdot 9-3\cdot8\)
2.2. \(\dfrac{\dfrac{4}{9}\cdot\dfrac{1}{7}}{\left(\dfrac{3}{7}-\dfrac{3}{2}\right)\cdot\dfrac{8}{3}}=\dfrac{4}{63}\cdot\dfrac{1}{-\dfrac{15}{14}\cdot\dfrac{8}{3}}=\dfrac{4}{63}\cdot\dfrac{1}{\dfrac{-20}{7}}\) -
Otázka 3 / 14
3. Otázka
Bodové ohodnocení: 2Vypočtěte a výsledek zapište zlomkem v základním tvaru:
(Zlomkovou čárku zapište pomocí lomítka, např. jednu polovina = 1/2)
\(\dfrac{1}{4}:(0,7+\dfrac{5}{4})\)Správně
Špatně
\(\dfrac{1}{4}:(\dfrac{7}{10}+\dfrac{5}{4})=\dfrac{1}{4}:\dfrac{14+25}{20}=\dfrac{1}{4}\cdot\dfrac{20}{39}\)
-
Otázka 4 / 14
4. Otázka
Bodové ohodnocení: 4Zjednodušte:
(výsledný výraz nesmí obsahovat závorky)4.1. \((4a+2)^2-4a(2+3a)\)
4.2. \((4-3c)\cdot\dfrac{c}{2}-\dfrac{2+c}{4}\)
Správně 4 / 4BodyŠpatně / 4 Body4.1. \(16a^2+16a+4-8a-12a^2\)
4.2. \(\dfrac{c(4-3c)}{2}-\dfrac{2+c}{4}=\dfrac{2c(4-3c)-(2+c)}{4}\) -
Otázka 5 / 14
5. Otázka
Bodové ohodnocení: 4Řešte rovnici:
5.1. \(2(x+2)=4\)
5.2. \(2\cdot\dfrac{a+4}{3}-2a=\dfrac{4}{6}a+\dfrac{6}{9}\)
Přiřaďte
- 0
- 1
- NŘ
- -1
- -36
- -5
- 5
-
5.1.
-
5.2.
Správně 4 / 4BodyŠpatně / 4 Body5.1. \(2x+4=4⇒2x=4-4\)
5.2. \(2\cdot\dfrac{a+4}{3}-2a=\dfrac{4}{6}a+\dfrac{6}{9}\:/\cdot 18\\
6\cdot2(a+4)-36a=12a+12\) -
Otázka 6 / 14
6. Otázka
Bodové ohodnocení: 2Roman, Pavel a Zdenek šetřili na dovolenou. Roman ušetřil 6 000 Kč. Zdenek ušetřil jednu třetinu úspor Pavla a Romana. Všichni tři dohromady ušetřili čtyřikrát více než Pavel.
Neznámý počet korun, které uspořil Pavel, označte písmenem p a sestavte k úloze odpovídající rovnici s neznámou p.
(Pokud se v zápise vyskytne zlomek, použijte k jeho zápisu lomítko /.
Pro správnou odpověď prosím napište rovnici v pořadí Roman, Pavel, Zdenek.)Správně
Špatně
Roman …… 6 000,-
Pavel …….. p
Zdenek …..1/3(p+6000)
celkem …… 4p -
Otázka 7 / 14
7. Otázka
Bodové ohodnocení: 2Pavel, Roman a Zdenek šetřili na dovolenou. Roman ušetřil 6 000 Kč. Zdenek ušetřil jednu třetinu úspor Pavla a Romana. Všichni tři dohromady ušetřili čtyřikrát více než Pavel. (viz. předchozí úloha)
Neznámý počet korun, které uspořil Pavel, označte písmenem p a vypočítejte, kolik korun naspořil Pavel.
Správně
Špatně
6000 + p + 1/3(p + 6000)=4p/*3
18000+3p+p+6000=12p -
Otázka 8 / 14
8. Otázka
Bodové ohodnocení: 3Přiřaďte správné odpovědi:
a) \(65 \:min \cdot\: ………… = 3\: hod – 50\: min\)
b) \(0,5\: kg : 50\: g + 200\: mg \cdot 2\: g = …………… g\)
c) \(100 \:cm^3-2 \:l+0,5\: hl = …………… dm^3\)
Přiřaďte
- 2
- 10,4
- 48,1
- 104
- 0,0481
- 3
- 1
- 50
- 0,05
- 1,04
- 1 040
-
a)
-
b)
-
c)
Správně 3 / 3BodyŠpatně / 3 Bodya) \(3\: hod – 50\: min=3\cdot60-50=130:65\)
b) \(0,5\: kg : 50\: g + 200\: mg \cdot 2\: g =500:50+0,2\cdot 2\)
c) \(100 \:cm^3-2 \:l+0,5\: hl =0,1-2+50\)
-
Otázka 9 / 14
9. Otázka
Bodové ohodnocení: 3Je dán čtverec ABCD. Úhlopříčka čtverce je \(\sqrt{32}\).

A) Vypočtěte délku strany čtverce.
B) Vypočtěte obsah vybarvené části obrazce.
- A) Délka strany čtverce je (4) j. B) Obsah vybarvené části obrazce je (3,4, 3,44) j2.
Správně 3 / 3BodyŠpatně / 3 BodyA) Úhlopříčka rozdělí čtverec na 2 rovnoramenné pravoúhlé trojúhelníky. Pomocí Pythagorovi věty umíme spočítat délku strany čtverce.
\((\sqrt{32})^2=a^2+a^2\)B) Nevybarvené části obrazce vytvoří kruh s průměrem o délce strany. Vypočítáme obsah čtverce, od něj odečteme obsah kruhu a máme výsledek.
-
Otázka 10 / 14
10. Otázka
Bodové ohodnocení: 4Stará fotografie měla rozměry a = 10 cm a b = 6 cm. Při kopírování vznikla nová fotografie. Oba rozměry byly zvětšeny 2,5krát.
Rozhodněte, zda jsou následující tvrzení pravdivá nebo nepravdivá. Do odpovědi zapište Ano/Ne.
- Rozměry nové fotografie jsou v poměru 3:5 (Ne, ne, NE) Obvod nové fotografie je 80 cm (Ano, ano, ANO)
Správně 4 / 4BodyŠpatně / 4 BodyRozměry nové fotografie jsou 10*2,5 a 6*2,5.
Rozměry můžeme zkrátit na základní tvar a dostaneme potřebný poměr.
Obsah vypočítáme podle vzorce pro obsah obdélníku. -
Otázka 11 / 14
11. Otázka
Bodové ohodnocení: 2Jaký je objem krabičky, která nám vznikne slepením ze sítě na obrázku?
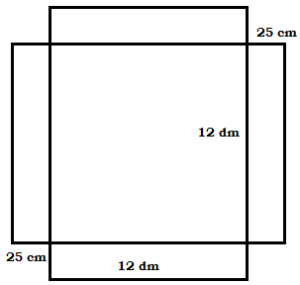 Správně
Správně
Špatně
Objem tělasa spočítáme jako obsah podstavy vynásobený výškou. Pozor na jednotky.
-
Otázka 12 / 14
12. Otázka
Bodové ohodnocení: 2Vypočtěte velikost úhlu \(\beta\):
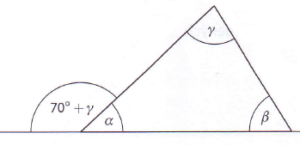 Správně
Správně
Špatně
Víme, že úhel na celé přímce má velikost 180°. Místo úhlu alfa dosadíme (180°-(70°+ gama)). Trojúhelník nám dá v součtu 180°.
180° – 70° – gama + gama + beta = 180° -
Otázka 13 / 14
13. Otázka
Bodové ohodnocení: 2Hrnec je do 2/3 naplněn vodou. Dno má obsah 250 cm2. Do hrnce přilijeme 0,035 hl vody. O kolik cm stoupne hladina vody v hrnci?
Správně
Špatně
To, že je hrnec naplněn do 2/3 nás při výpočtu nezajímá. 0,035 hl je objem, který přiléváme a známe obsah podstavy. Dosadíme do vzorce pro výpočet objemu a získáme výšku.
-
Otázka 14 / 14
14. Otázka
Bodové ohodnocení: 6Vypočtěte a doplňte následující:
- Z 1 tuny cukrovky se vyrobí 200 kg cukru. K výrobě 0,6 tuny cukru, je potřeba 100 kg vody. Na 150 kg vody je potřeba (4500, 4 500) kg cukrovky. Zimní bunda stála 1 200 Kč. Byla zlevněna o 15 % a poté ještě jednou. Konečná cena bundy je 918 Kč. Při druhé slevě byla bunda zlevněna o (10) %. Cena sušenek byla před zdražením 15 Kč. Zdražení bylo ve výši 20 %. Po zdražení sušenky stojí (18) Kč.
Správně 6 / 6BodyŠpatně / 6 Body- Pomocí trojčlenky určíme, kolik cukrovky potřebujeme k výrobě 0,6 t cukru. Zjištěnou hodnotu dosadíme do druhé trojčlenky, pomocí níž získáme, kolik cukrovky je potřeba na 150 kg vody.
- Spočítáme cenu bundy po slevě. Tato cena bude v dalším výpočtu základ (100%) a dopočítáme procenta pro konečnou cenu.
- Pokud zdražujeme, můžeme spočítat dané procento a částku přičíst k původní, nebo můžeme rovnou spočítat cenu po zdražení (120%).
