
Nerovnice
Řešení lineárních nerovnic, zápis pomocí intervalů …
100 Kč
Popis
V online kurzu si zopakujete řešení lineárních nerovnic. Příklady se mohou objevit u přijímacích zkoušek na střední školu.
Najdete zde 3 příklady písemně komentované, 10 řešených a 10 příkladů k procvičení.
Online kurz máte k dispozici po dobu jednoho měsíce.
Najdete zde např.:
1) Vyřeš nerovnici
\(\dfrac{x-2}{2}≤\dfrac{2x-1}{3}-\dfrac{x-2}{4}\)
2) Pro \(z\in N<3 \) vyřeš nerovnici a proveď zkoušku
\(z-(5+z)≥-\dfrac{z}{2}-6\)
3) Vyřeš nerovnici
\(3(a-5)≤\dfrac{a+2}{2}>4(2a-1)\)
Ukázka z kurzu
Vyřeš nerovnici a proveď zkoušku
\(6x-5>10+3x\)
Neznámou máme na levé i pravé straně, proto naše první úprava bude spočívat v tom, že dáme na jednu stranu neznámou a na stranu druhou čísla. Nesmíme zapomenout na to, že při přechodu přes znaménko nerovnosti měníme znaménka. Dostaneme
\begin{eqnarray*}6x-5&>&10+3x\\
6x-3x&>&10+5\end{eqnarray*}
Hodnoty na pravé i levé straně nerovnice spočítáme a dostáváme
\begin{eqnarray*}6x-3x&>&10+5\\
3x&>&15\end{eqnarray*}
Stejně jako u rovnic, i zde platí, že výsledkem nerovnice je až samotné x. Proto celou rovnici podělíme 3 a dostaneme již konečný výsledek.
\begin{eqnarray*}3x&>&15\:/:3\\
\dfrac{3x}{3}&>&\dfrac{15}{3}\\
x&>&5\end{eqnarray*}
Výsledek zakreslíme na osu a zapíšeme výsledný interval.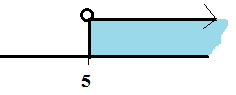
$$x\in (5; \infty)$$
Zkoušku a další příklady najdete v placené verzi.

