Kurz k přijímacím zkouškám na SŠ
V kurzu k přijímacím zkouškám na střední školu najdete řešené ukázkové příklady, které se v přijímačkách mohou objevit. Pokud si projdete všechny příklady a spočítáte je, gratulujeme, u přijímací zkoušky z matematiky by vás nemělo nic překvapit. Jestliže u některého příkladu nebudete vědět, jak jej spočítat, kliknutím na odkaz si můžete zakoupit kurz, který obsahuje právě tento typ příkladů. Po absolvování vybraného kurzu budete připraveni na úspěšné zvládnutí přijímaček z matematiky.
V nabídce máme i kompletní kurz k přijímacím zkouškám, který zahrnuje všechny typy příkladů, se kterými se u zkoušky můžete setkat.
Příklad 1: Obvody a obsahy obrazců
Zadání: Vypočítej obsah vybarvené části rovnostranného trojúhelníku. Základna je dlouhá 5\(\nobreakspace\)dm. Vrcholy trojúhelníku tvoří středy jednotlivých částí kružnic. 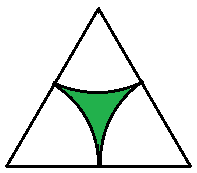
Kurz na obvody a obsahy obrazců
Kurz na vyjádření neznámé ze vzorce
Máme rovnostranný trojúhelník a vrcholy tvoří středy kružnic. Jestliže části kružnic složíme k sobě, dostaneme půlkruh. Vypočítáme obsah trojúhelníku, od něho odečteme obsah půlkruhu a budeme mít řešení.
\(r=\dfrac{a}{2}=\dfrac{5}{2}=2,5\:dm\)
\begin{eqnarray*}S_{k}&= &\dfrac{\pi \cdot r^{2}}{2}\\[2ex]
S_{k}&= &\dfrac{\pi \cdot (2,5)^{2}}{2}\\[2ex]
S_{k}&= &\dfrac{\pi \cdot6,25}{2}\\[2ex]
S_{k}&= &\dfrac{19,625}{2}=9,813\:dm^{2}\end{eqnarray*}
\begin{eqnarray*}a^{2}&= &v^{2}+\left(\dfrac{a}{2}\right)^{2}\\[2ex]
5^{2}&= &v^{2}+\left(\dfrac{5}{2}\right)^{2}\\[2ex]
25&= &v^{2}+6,25\\
25-6,25&= &v^{2}\\
18,75&= &v^{2}\:/\cdot \sqrt{\:\:}\\
\sqrt{18,75}&= &v\\
v&= &4,33\:dm\end{eqnarray*}
\begin{eqnarray*}S_{t}&= &\dfrac{a \cdot v_{2}}{2}\\[2ex]
S_{t}&= &\dfrac{5 \cdot 4,33}{2}\\[2ex]
S_{t}&= &\dfrac{21,65}{2}\\[2ex]
S_{t}&= &10,83\:dm^{2}\end{eqnarray*}
$$S_{t}-S_{k}=10,83-9,812=1,018\:dm^{2}$$
Obsah vybarvené části je \(1,018\: dm^{2}\).
Kurz na obvody a obsahy obrazců
Kurz na vyjádření neznámé ze vzorce
Příklad 2: Poměr
Zadání: Fotografie s rozměry 12 cm a 20 cm chceme upravit v poměru
a) 2 : 6,
b) 5 : 4.
Jak velká bude fotografie po úpravách? Došlo ke zmenšení nebo zvětšení?
Kurz na výpočet poměrů
a) Poměr je menší než 1, tzn., že se jedná o zmenšení.
$$12 \cdot \dfrac{2}{6} = \dfrac{24}{6} = 4\\
20 \cdot \dfrac{2}{6} = \dfrac{40}{6} = 6,7$$
Nové rozměry fotografie po zmenšení jsou 4 cm a 6,7 cm.
b) Poměr je větší než 1. Jedná se o zvětšení.
$$12 \cdot \dfrac{5}{4} = \dfrac{60}{4} = 15\\
20 \cdot \dfrac{5}{4} = \dfrac{100}{4} = 25$$
Po zvětšení má fotografie rozměry 15 cm a 25 cm.
Příklad 3: Měřítko mapy
Zadání: Chodec ujde 2,4 km za 12 minut. Trasa, kterou ujde za 25 minut, na mapě měří 10\(\nobreakspace\)cm. Jaké je měřítko mapy? Rychlost chodce se nemění.
Kurz na měřítko mapy
$$1 \:km \:za\: min = \dfrac{2,4}{12}\cdot \dfrac{10}{10}=\dfrac{\color{blue}{24}}{\color{blue}{120}}=\dfrac{2}{10} =0,2\\[4ex]
km\:za\: 25\:min = 0,2\cdot 25 = 5\:km\\[4ex]
10 :500\:000\qquad /:10\\
1:50\:000\qquad\qquad$$
Měřítko mapy je 1 : 50 000.
Příklad 4: Povrch a objem hranolu
Zadání: Bazén tvaru kolmého hranolu se dnem tvaru rovnoramenného lichoběžníku s rozměry základen 12 m a 160 dm a rameny 800 cm je hluboký 2 m. Při jarním úklidu je třeba vybělit dno a stěny bazénu. Kolik \(m^{2}\) je třeba vybělit?
Kurz na výpočet povrchu a objemu hranolu
Kurz na vyjádření neznámé ze vzorce
\(a=12\:m\\
b=d=800\:cm = 8\:m\\
c=160\:dm=16\:m\\
v=2\:m\\
S=\:?\)
$$S=S_{p}+S_{pl}$$
\begin{eqnarray*}S_{p}&= &=\dfrac{(a+c)\cdot v}{2}\\
S_{p}&= &\dfrac{(12+16)\cdot v}{2}\end{eqnarray*}
Neznáme výšku lichoběžníku, ale umíme ji spočítat pomocí Pythagorovi věty. Jedná se o\(\nobreakspace\)rovnoramenný lichoběžník, proto od delší strany základny odečteme menší délku základny. Zbytek podělíme dvěmi a dostaneme délku strany pravoúhlého trojúhelníku. Přeponu trojúhelníku tvoří rameno lichoběžníku a druhá odvěsna bude naše potřebná výška.
$$x=\dfrac{16-12}{2}=4:2=2\:m$$
\begin{eqnarray*}b^{2}&= &x^{2}+v^{2}\\
8^{2}&= &2^{2}+v^{2}\\
64&= &4+v^{2}\\
64-4&= &v^{2}\:/\cdot \sqrt{\:\:}\\
v&= &\sqrt{60}\doteq 7,8\:m\end{eqnarray*}
\begin{eqnarray*}S_{p}&= &\dfrac{(12+16)\cdot v}{2}\\
S_{p}&= &\dfrac{(\color{blue}{28})\cdot 7,8}{\color{blue}{2}}\\
S_{p}&= &14\cdot 7,8\\
S_{p}&= &109,2\:m^{2}\end{eqnarray*}
\begin{eqnarray*}S_{pl}&= &o_{p}\cdot v\\
S_{pl}&= &(a+b+c+d)\cdot v\\
S_{pl}&= &(16+8+12+8)\cdot 2\\
S_{pl}&= &44\cdot 2\\
S_{pl}&= &88\:m^{2}\end{eqnarray*}
$$S=S_{p}+S_{pl}=109,2+88=197,2\:m^{2}$$
Je třeba vybělit \(197,2\:m^{2}\) plochy.
Kurz na výpočet povrchu a objemu hranolu
Kurz na vyjádření neznámé ze vzorce
Příklad 5: Povrch a objem válce
Zadání: Máme dvě různé nádoby tvaru válce. V nádobě s vnitřním průměrem 8 cm a výškou 6\(\nobreakspace\)cm máme roztok, který chceme přelít do jiné nádoby s vnitřním poloměrem 3 cm. Jak vysoko bude roztok v druhé nádobě? Výsledek zaokrouhli na jedno desetinné místo.
Kurz na výpočet povrchu a objemu válce
Kurz na vyjádření neznámé ze vzorce
\(d_{1}=8\:cm⇒r_{1}=4\:cm\\
v_{1}=6\:cm\\
r_{2}=3\:cm\\
v_{2}=\:?\)
\begin{eqnarray*}V_{1}&= &S_{p}\cdot v= \pi r^{2}v\\
V_{1}&= &3,14 \cdot 4^{2}\cdot 6\\
V_{1}&= &3,14 \cdot 16 \cdot 6\\
V_{1}&= &301,44\:cm^{3}\end{eqnarray*}
\begin{eqnarray*}V_{2}&= &S_{p}\cdot v= \pi r^{2}v\\
301,44&= &3,14 \cdot 3^{2}\cdot v\\
301,44&= &3,14 \cdot 9 \cdot v\\
301,44&= &28,26\cdot v\:/:28,26\\
301,44:28,26&= &v\\
v&= &10,666667 \doteq 10,7\:cm\end{eqnarray*}
Roztok v druhé nádobě dosahuje výšky 10,7 cm.
Kurz na výpočet povrchu a objemu válce
Kurz na vyjádření neznámé ze vzorce
Příklad 6: Převody jednotek
Zadání:Tři úplně stejné hlávky zelí váží celkem 6 600 g. Pět stejných hlávek kapusty váží celkem 10,25 kg. Je těžší hlávka zelí nebo kapusty a o kolik kilo?
Kurz na převody jednotek
a) zelí
$$6\: 600\: g : 3\: ks = 2\:200\: g/ks$$
b) kapusta
$$10,25\: kg=10\: 250\: g\Rightarrow 10\: 250\: g : 5\:ks = 2\:050\: g/ks$$
$$2\:200- 2\:050=150\: g=0,15\: kg$$
Hlávka zelí je těžší než kapusty o 0,15 kg.
Příklad 7: Převody jednotek
Zadání:\(53,575\:l + 30,9 \:dm^3 + 1\: 459\:mm^3 = ……………………. cm^3\)
30\color{red}{,9} \:dm^3=30\:\color{red}{900,}\:cm^3\\
459\color{green}{,0}\:mm^3=0\color{green}{,459}\:cm^3\\
53,575\:l + 30,9 \:dm^3 + 1\: 459\:mm^3 = 53\:575+30\:900+0,459=84\:475,459\:cm^3$$
Příklad 8: Přímá a nepřímá úměra
Zadání: Montujeme zahradní skleník. Dva dělníci provedou montáž za 54 hodin. Za jaký čas provede montáž 9 dělníků?
Kurz na přímou a nepřímou úměru
Čím více dělníků, tím méně hodin ⇒ nepřímá úměra.
\begin{array}{ccl}
\text{2 dělníci} & \text{……………………} & \text {54 hodin} \\
\text{↓ 9 dělníků} & \text{……………………}& \text {x hodin ↑} \\
\hline
\end{array}
$$\begin{eqnarray*} x&=& \dfrac{\color{red}{54} \cdot 2}{\color{red}{9}}\\[4ex]
x&=&\dfrac{6\cdot 2}{1}\\[4ex]
x&=&6\cdot 2 =12\end{eqnarray*}$$
9 dělníků provede montáž skleníku za 12 hodin.
Příklad 9: Procenta
Zadání: Ve třídě je 14 dívek. Kolik je ve třídě chlapců, jestliže tvoří 44 % žáků třídy?
Kurz na výpočet procent
Procenta ⇒ přímá úměra.
Možno řešit dvěma způsoby, pokud Vás, stejně jako mě, hned nenapadne lehká varianta:
A) lehké řešení
→ 100 % – 44 % = 56 % tvoří dívky
\begin{array}{ccl}
\text{56 %} & \text{……………………} & \text {14 dívek} \\
\text{↑ 100 %} & \text{……………………}& \text {x dětí ↑} \\
\hline
\end{array}
$$\begin{eqnarray*} x&=& \dfrac{\color{blue}{14} \cdot 100}{\color{blue}{56}}\\[4ex]
x&=&\dfrac{2\cdot \color{orange}{100}}{\color{orange}{8}}\\[4ex]
x&=&\dfrac{\color{red}{2}\cdot 25}{\color{red}{2}}\\[4ex]
x&=&25\end{eqnarray*}$$
Ve třídě je celkem 25 žáků. Jestliže je tam 14 dívek, chlapců je 11.
Příklad 10: Rovnice
Zadání: Vyřeš rovnici a proveď zkoušku:
$$\dfrac{3}{4}(2u-5)-\dfrac{u}{3}-\dfrac{1}{20}=\dfrac{4}{5}(3u-2)-\dfrac{2}{3}(5u-3)$$
Kurzy na lineární rovnice
\begin{eqnarray*}
\dfrac{3}{4}(2u-5)-\dfrac{u}{3}-\dfrac{1}{20}&=&\dfrac{4}{5}(3u-2)-\dfrac{2}{3}(5u-3)\:/\cdot 60\\[2ex]
\dfrac{\color{blue}{60}\cdot3}{\color{blue}{4}}(2u-5)-\dfrac{\color{red}{60}\cdot u}{\color{red}{3}}-\dfrac{\color{green}{60}\cdot1}{\color{green}{20}}&=&\dfrac{\color{orange}{60}\cdot4}{\color{orange}{5}}(3u-2)-\dfrac{\color{purple}{60}\cdot2}{\color{purple}{3}}(5u-3)\\[2ex]
15(6u-15)-20u-3&=&12(12u-8)-20(10u-6)\\
90u-225-20u-3&=&144u-96-200u+120\\
70 u +56u&=&24+228\\
126u&=&252\:/:126\\[2ex]
u&=&2\end{eqnarray*}
\begin{eqnarray*}
Zk: L&=& \dfrac{3}{4}(2u-5)-\dfrac{u}{3}-\dfrac{1}{20}= \dfrac{3}{4}(2\cdot2-5)-\dfrac{2}{3}-\dfrac{1}{20}= \dfrac{3}{4}(-1)+\dfrac{-2\cdot 20-3\cdot1}{60}=\\[2ex]&=&\dfrac{-3}{4}-\dfrac{43}{60}=\dfrac{-3\cdot15-43}{60}=\dfrac{-88}{60}=\dfrac{-22}{15}\\[2ex]
P&=&\dfrac{4}{5}(3u-2)-\dfrac{2}{3}(5u-3)=\dfrac{4}{5}(3\cdot2-2)-\dfrac{2}{3}(5\cdot2-3)=\dfrac{4}{5}(4)-\dfrac{2}{3}(7)=\\[2ex]&=&\dfrac{16\cdot3-14\cdot5}{15}=\dfrac{48-70}{15}=\dfrac{-22}{15}\\[2ex]
L&=&P\end{eqnarray*}
Příklad 11: Mnohočleny
Zadání: Rozlož na součin mnohočlenů pomocí vzorců: \(81m^4-9n^2\)
Řešení:
Podle vzorečků, které zatím umíme, nejvíc přichází v úvahu vzoreček: \((a^2-b^2)=(a-b)\cdot (a+b)\). U další dvou vzorečků máme 3 členy, zatímco v zadání jsou pouze 2:
$$81m^4-9n^2={(9m^2)}^2-{(3n)}^2=(9m^2-3n)\cdot (9m^2+3n)$$
Příklad 12: Nerovnice
Zadání: Vyřeš nerovnici \(8-3x>\dfrac{x+2}{3}≤\dfrac{3x+4}{4}\)
\begin{array}{rcl rcl}
8-3x&>&\dfrac{x+2}{3}\:/\cdot 3& \qquad\qquad \dfrac{x+2}{3}&≤&\dfrac{3x+4}{4} \:/\cdot 12\\[2ex]
3\cdot (8-3x)&>&\dfrac{\color{blue}{3}(x+2)}{\color{blue}{3}} & \qquad\qquad \dfrac{\color{red}{12}(x+2)}{\color{red}{3}}&≤&\dfrac{\color{green}{12}(3x+4)}{\color{green}{4}} \\[2ex]
24-9x&>&x+2 & \qquad\qquad 4(x+2)&≤&3(3x+4) \\
-9x-x&>&-24+2 & \qquad\qquad 4x+8&≤&9x+12 \\
-10x&>&-22\:/:(-10) & \qquad\qquad 4x-9x&≤&-8+12 \\
x&<&2,2& \qquad\qquad -5x&≤&4\:/:(-5) \\
&&&x&≥&\dfrac{-4}{5} \\[2ex]
x_{1}\in (- \infty;2,2)&&&x_{2}\in \left(- \dfrac{4}{5};\infty\right)\end{array}
$$x\in x_{1}\cap x_{2} ⇒ (- \infty;2,2)\cap \left(- \dfrac{4}{5};\infty\right)\\[2ex]
x\in \left(- \dfrac{4}{5};2,2\right)$$
Příklad 13: Soustava rovnic
Zadání: Na dvorku jsou holubi a králíci. Všechna zvířata mají dohromady 35 hlav a 110 nohou. Kolik je na dvoře holubů a kolik králíků?
Zápis:
– holuby označíme x
– králíky označíme y
– každé zvíře má 1 hlavu, holubi mají 2 nohy, králíci 4 nohy
\begin{array}{lcl}
\text{holubi v ks } & \text{ ……………………} & \text {x} \\
\text{králíci v ks} & \text{……………………}& \text {y} \\
\text{celkem ks = hlav} & \text{……………………} & \text {35} \\
\text{počet noh holubů} & \text{……………………} & \text {2x} \\
\text{počet noh králíků} & \text{……………………}& \text {4y} \\
\text{celkem noh} & \text{……………………} & \text {110} \\
\hline
\end{array}
Sestavíme rovnici a vyřešíme.
$$\begin{eqnarray*}x+y&=&35\:/\cdot (-2)\qquad\qquad\qquad\qquad(*)\\
2x+4y&=& 110\\\\[2ex]
-2x-2y&=&-70\\
2x+4y&=& 110\\\\[2ex]
-2x+2x-2y+4y&=&-70+110\\
2y&=&40\:/:2\\
y&=&20\\\\[4ex]
x+y&=&35\\
x+20&=&35\\
x&=&35-20\\
x&=&15\end{eqnarray*}$$
Řešení je [15; 20] a uděláme zkoušku:
$$\begin{eqnarray*}
Zk:L_{1}&=&x+y=15+20=35\\
P_{1}&=&35\\
L_{2}&=&2x+4y=2\cdot15+4\cdot20=30+80=110\\
P_{2}&=&110\\
L&=&P\end{eqnarray*}$$
Na dvoře je 15 holubů a 20 králíků.
Příklad 14: Zlomky
Zadání: Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac{\left(2\dfrac {1}{5}\cdot 3\dfrac {8}{6}\right)}{5\dfrac {2}{3}}\)
$$\dfrac{\left(\color {red}{2}\dfrac {1}{\color {blue}{5}}\cdot \color {green}{3}\dfrac {8}{\color {orange}{6}}\right)}{\color {violet}{5}\dfrac {2}{\color {brown}{3}}}=\dfrac{\dfrac {\color {red}{2}\cdot \color {blue}{5}+1}{\color {blue}{5}}\cdot \dfrac {\color {green}{3}\cdot \color {orange}{6}+8}{\color {orange}{6}}}{\dfrac {\color {violet}{5} \cdot\color {brown}{3}+2}{\color {brown}{3}}}=\dfrac{\dfrac {11}{5}\cdot\dfrac {26}{6}}{\dfrac {17}{3}}=\dfrac{\dfrac {11\cdot26}{5\cdot6}}{\dfrac {17}{3}}=\dfrac {286}{30}:\dfrac {17}{3}=\dfrac {286}{\color {orange}{30}}\cdot\dfrac {\color {orange}{3}}{17}=\dfrac {\color {red}{286}}{\color {red}{10}}\cdot\dfrac {1}{17}=\\[6ex]=\dfrac {143}{5}\cdot\dfrac {1}{17}= \dfrac {143\cdot 1}{5\cdot 17}=\dfrac {143}{85}$$
Příklad 15: Celá čísla
Zadání: Vypočítej:
\((6-\sqrt {9})^2-(\sqrt {25})^2\)
$$(6-\color{blue}{\sqrt {9}})^2-(\color{red}{\sqrt {\color{green}{25}}})\color{red}{^2}=(6-\color{blue}{3})^2-\color{green}{25}=(3)^2-25=9-25=-16$$
